－恒星の大きさと質量－

恒星を理解する重要な要素として、その大きさ・質量を見積ることがあります。しかし恒星は我々の地球から遠く離れているため、これらの量を正確に見積ることは、そう簡単ではありません。ここでは、大きさ・質量を見積る手法について学習します。

恒星の大きさ
干渉計 を用います。
比較的近距離にあり、直系の大きい恒星に対しては、望遠鏡に 干渉計 を取り付けることにより大きさを直接測定できます。このようにして求められた大きさを、視直径といいます。

ＨＲ図 から求めます。
同じスペクトル型の恒星では、明いものほど半径が大きいはずです。また明るさが同じなら、表面温度の低いものほど半径が大きいはずです。つまりHR図の特性から、右上にいくほど恒星の半径は大きく、左下ほど小くなります。この性質を用いて、恒星の大きさを求めることが可能となります。

恒星の半径とＨＲ図

Ｓ：太陽の半径
Ｒ：恒星の半径

主系列星の半径

太陽の０．１倍～１０倍の範囲内
表面温度：高　⇒　半径：大

巨星・超巨星の半径

巨星：１０倍～１００倍
超巨星：１００倍～　以上

白色矮星の半径

太陽の０．０１倍程度

恒星の質量
連星から求めます。
２つ以上の恒星が互いの周りを公転しているものを、連星といいます。
連星には望遠鏡で直接分るものの他に、スペクトル観測で判明するものもあります。また変光星として観測できるものがあります。恒星の約半分は連星 であると考えられています。
さて注目している恒星が連星の場合は、ケプラーの第３法則よりその質量を求めることができます。

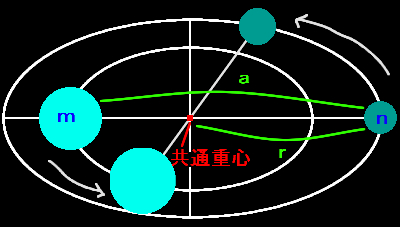主星：明るいほうの恒星　⇒　質量：ｍ
伴星：暗いほうの恒星　　 ⇒　質量：ｎ
主星・伴星間の平均距離：ａ
公転周期：Ｐ

ケプラーの第３法則より

ａ

３

/ Ｐ

２

＝Ｇ（ｍ + ｎ） / ４π

２

が成り立ちます。　

また、重心からの距離は質量に反比例するので、

ｍ（ａ－ｒ）＝ｎｒ

となるので、　

以上２式より、Ｐ・ａ・ｒは観測により分かるので、ｍ・ｎを未知とする連立方程式により質量を求めることはできます。

※詳しいことは地学2にて取り扱います。

註 食連星とはなにか
視線方向と連星の公転面が並行の場合、恒星の明るさが変化する現象が起こります。このような連星を食連星といいます。

１の状態のとき、伴星が主星を隠すためかなり暗くなります。
２の状態のとき、主星が伴星を隠すため若干暗くなります。

質量－光度関係 から求めます。
連星ではない恒星に関しては、その質量を求める直接的な方法がありません。しかし連星系をなしている恒星のでは、以下に示す質量－光度関係が成立していることがわかっています。連星以外の主系列星についてもこの関係が成立していると仮定すると、絶対等級から恒星の質量を求めることが可能になります。

質量－光度関係

主系列星の絶対等級は、質量の３～４乗に比例します。