−惑星の軌道運動−
この節では、惑星の軌道運動の基礎として、ケプラーの法則を学びます。ケプラー以前の天文学は「完全なる神は完全なる運動を造られる」という観点から、惑星は中心の星の周囲を完全な円軌道で運行すると考えられていました。これは地上は始まりと終わりのある不完全な直線運動、天上は始まりも終わりもない円運動、という古代ギリシャ以来の考え方です。
ケプラーはこの定説を打ち破り、後にケプラーの法則と呼ばれるものを打ち立てました。その詳細は、以下のとおりです。
ケプラーの法則
第1法則<楕円軌道の法則>
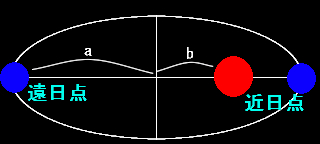
惑星は太陽を1つの焦点とする楕円軌道を描きます。
| 遠日点 |
最も太陽から遠ざかる地点のこと。 |
| 近日点 |
最も太陽に近づく地点のこと。 |
| 平均距離 |
遠日点と太陽までの距離と、近日点と太陽までの距離の平均の値です。
aに相当します。<地球…約1.5km = 1天文単位> |
| 離心率 |
e = b/a (0
<= e < 1) で表されます。
離心率が大きなものほど、軌道は偏平な楕円になります。 |
第2法則<面積速度一定の法則>
太陽と惑星を結ぶ直線(動径)は、 等しい期間に等しい面積を描きます。
→公転速度は一定ではないことがわかります。
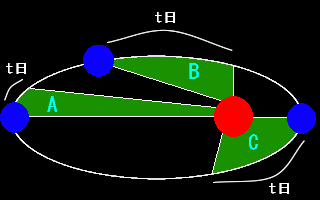 |
A = B = C
近日点…最も速度が速くなります。
遠日点…最も速度が遅くなります。 |
第3法則<調和の法則>
惑星と太陽の平均距離の3乗は、 その惑星の公転周期の2乗に比例します。
ケプラーの法則のまとめ
ケプラーの3法則の特徴を言い表しますと、次のようになります。つまり
| 第1法則…軌道の形 |
| 第2法則…軌道上の速さ |
| 第3法則…軌道の大きさ |
|
をそれぞれが表しています。 |
⇒このケプラーの法則は惑星だけでなく 小惑星・彗星に対しても有効です。
|







